1-Introduction
Local Stresses Based on Chocking Model
Chocking model is a model in which pipe shell is chocked under a radial force as shown in figure 1.

Figure 1: Chocking model in which pipe is choked at radial loads location
At radial force location a discontinuity area is formed. So, local stresses are created at that place. In this section a method is introduced for the local stresses calculation. Moreover, width of discontinuity area in which the local stresses are effective is calculated.
The radial load exerted on pipe shell produces the following forces on the pipe shell:
-
Longitudinal bending moment: As shown in figures 2 and 3, these moments have a tendency to bend each element strip of pipe toward the chocked pipe diameter. This moment is considered the source of longitudinal local bending stress.

Figure 2: Longitudinal bending moment and stress
-
Circumferential compressive force: As shown in figure 3, the radial force creates a load which resists against any deformation in circumferential direction. Without this force, cross section at discontinuity area collapses under the radial force. This force is source of circumferential local membrane stress (figure 3).

Figure 3: Longitudinal bending and circumferential membrane stresses
The chocking model is basis of Kellogg’s model which has been successfully used to calculate local stress at pipe-support junctions for many years in piping industries. The support can be a structural profile or a pipe which is welded to a pipe shell. Moreover, the allowable nozzle loads defined by API 650 are based on circumferential local membrane stress which is extracted by the chocking model.
2-Local stress calculation
For calculation of the local stresses, the mentioned loads which create these stresses should be determined at first. In beam equations, shear force function is not continuous in a place where an external shear force is applied. So it is not possible to calculate internal bending moment at that place with normal beam equations. Therefore, a method which enables us to calculate internal bending moment in a discontinuity location should be used. One of suitable models which give us internal forces in that location is “beam on elastic foundation”. As mentioned before, the bending moment tends to bend all element strip of a pipe locally, as shown in figure 2. If it is proved the radial force is proportional to radial deflection for the element strip, the beam on elastic foundation model in which the elastic support is proportional to the vertical deformation can be used. Because our primary attention is local stresses which exist in discontinuity area, the pipe is assumed the infinite. It is assumed the radial loads are uniformly and symmetrically distributed on the pipe shell.
A strip of element is shown in Figure 4.

Figure 4: Loads on a strip of element

(1)
(2)
(3)
From (2) and (3):

(4)
(5)
From (5) and (4):
(6)
From applying Hook’s law in circumferential direction:

(7)
(8)
From (7) and (8):
(9)
From (6) and (9):

(10)
Equation (10) shows that is proportional to ΔR.
Now beam on an elastic foundation can be used to simulation as follows.
Referring to case 10 from table 8 of [7], Roark’s has given the following formula to find internal forces for an infinite beam on an elastic foundation:

Figure 5: Infinite beam on an elastic foundation

(11)
(12)
(13)
In which

(14)
is defined as foundation modulus (unit stress per unit deflection)
is defined as beam width
With determining of for the chocking model, equation (13) can be used for finding bending moment at x=0 where the load is applied.
(15)
2-1-β Calculation

(16)
(17)
E’ is elasticity module of the beam on an elastic foundation. Stresses in this model do not produce any stresses in other directions because the lateral face of beam in z direction can move freely (figure 5). But in the chocking mode, any deformation in longitudinal direction causes stress in circumferential direction because material in circumferential direction faces a resistance against any movement. So for using the beam model in which its lateral face freely moves an equivalent elasticity module should be developed for substituting in equation (14).
From applying Hook’s law on chocking model (figure 4):

(18)
(19)
From (18) and (19):
(20)
Referring to figure 5, I is calculated as follows:
(21)
From equations (16), (17), (20), (21) and (14):
(22)
From equations (10) and (22):
(23)
(24)
2-2-Bending moment calculation:
From equations (15) and (24):
(25)
2-3-Longitudinal Bending Stress
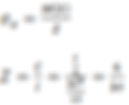
(26)
(27)
From equations (26) and (27):
(28)
can be defined as f: load per unit length around the pipe shell. so,
(29)
2-4-Circumferential membrane Stress
This local stress is uniformly applied in circumferential direction and considered as a membrane stress:
(30)
From equations (9) and (30):
(31)
can be calculated by equation (11) at x=0:
(32)
From equations (20), (21), (22) and (23):
(33)
From equations (33) and (31):
(34)
3-Discontinuity width
Equation (13) implies internal moment has its maximum at x=0 where the load is exerted and it starts to decrease with x increases. It means local stresses which are function of the internal moment are not effective in a location far away from the load location. But how far is acceptable for being out of danger area? It plays an important role in determining pad length calculation. Equations (12) and (13) shows the internal moment and shear force decrease significantly at a place where .

(35)
(36)
(37)
(39)
(38)

